原子軌道 １ｓ、２ｓ、２ｐ、３ｄ を導出は次の手順で行われる。
（１）　動径波動関数の導出
（２）　球面調和関数の導出
（３）　原子軌道の導出

ｎ＝主量子数、ｌ=方位量子数、ｍ=磁気量子数

方位量子数 ｌ＝０ の軌道をｓ軌道
方位量子数 ｌ＝１ の軌道をｐ軌道
方位量子数 ｌ＝２ の軌道をｄ軌道

さらに、次のように分類する。
１ｓ軌道　（ｎ、ｌ、ｍ）＝（１、０、０）
２ｓ軌道　（ｎ、ｌ、ｍ）＝（２、０、０）
２ｐ軌道　（ｎ、ｌ、ｍ）＝（２、１、０）
２ｐ軌道　（ｎ、ｌ、ｍ）＝（２、１、１）
２ｐ軌道　（ｎ、ｌ、ｍ）＝（２、１、-１）
３ｓ軌道　（ｎ、ｌ、ｍ）＝（３、０、０）
３ｐ軌道　（ｎ、ｌ、ｍ）＝（３、１、０）
３ｐ軌道　（ｎ、ｌ、ｍ）＝（３、１、１）
３ｐ軌道　（ｎ、ｌ、ｍ）＝（３、１、-１）

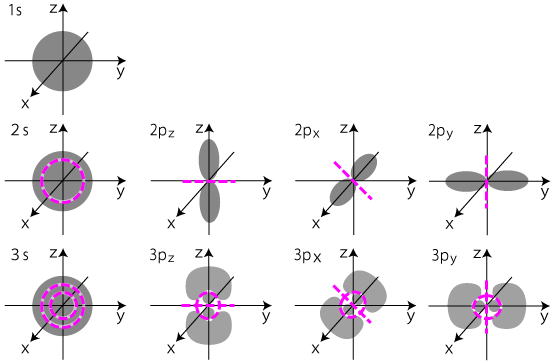
節面の数 ＝ 主量子数 − 1
方位量子数が増えると、球面状の節面が減り、非球面の節面が増える。


詳しくは、量子化学を勉強する必要があります。